Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 자바의 정석
- 웹개발
- 백준
- 브루트 포스
- 네트워크
- 코딩테스트
- JPA
- 면접
- 스프링
- 코테
- 객체지향프로그래밍
- programmers
- 스프링 MVC
- Bean Validation
- 자료구조
- 자바
- OS
- 쿼리dsl
- 운영체제
- 반복문
- db
- Java
- 프로그래머스
- 메서드
- 정처기
- ModelAttribute
- 스프링MVC
- 검증
- 스파르타코딩
- 알고리즘
Archives
- Today
- Total
개발일지
그래프 본문
728x90
목차
그래프란?
그래프는 정점(node 또는 vertex)과 간선(edge)로 이루어진 자료구조이다.
그래프의 활용
그래프는 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료구조이다. 그래서 그래프는 실생활에서 지하철 노선도 최단 경로, 도로, 선수 과목 등에 쓰이고 있다.
그래프 관련용어
- 간선(Edge) : 정점(노드)를 연결하는 선. 링크(Link) 또는 브랜치(branch) 로도 불린다.
- 인접 정점(adjacent vertex): 간선에 의해 직접 연결된 정점을 의미한다.
- 단순 경로(simple path) : 경로 중에서 반복되는 정점이 없는 경우를 의미한다. 한붓 그리기와 같이 같은 간선을 지나가지 않는 경로를 의미한다.
- 차수(degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수를 의미한다.
- 진출 차수(in-degree) : 방향 그래프에서 외부로 향하는 간선의 수를 의미한다.
- 진입 차수(out-degree): 방향 그래프에서 외부에서 들어오는 간선의 수를 의미한다.
- 경로 길이(path length) : 경로를 구성하는데 사용된 간선의 수를 의미한다.
- 사이클(cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우를 의미한다.
그래프 종류
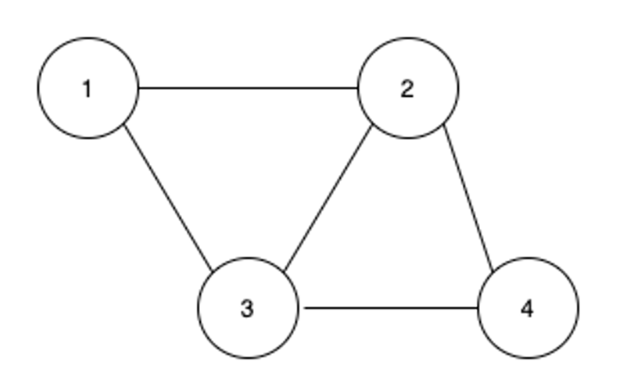
1. 무방향 그래프

- 두 정점을 연결하는 간선에 방향이 없는 그래프이다
- 최대 간선 수 : n(n-1) / 2
2. 방향 그래프
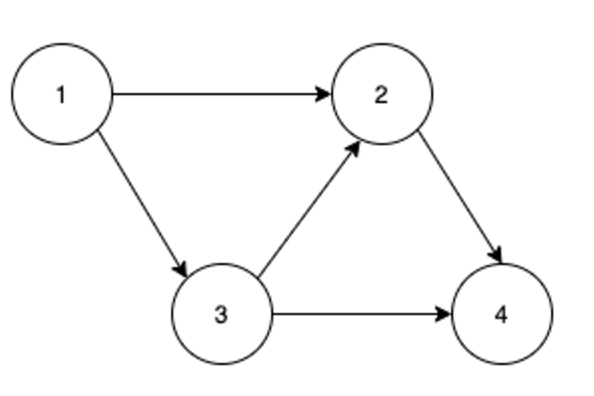
- 두 정점을 연결하는 간선에 방향이 존재하는 그래프로, 간선이 가리키는 방향으로만 이동할 수 있다.
- 최대 간선 수 : n(n-1)
3. 가중치 그래프

- 정점을 연결하는 간선에 가중치를 할당한 그래프이다.
4. 완전 그래프

- 모든 정점이 간선으로 연결된 그래프이다.
그래프 구현 방법
인접 행렬 또는 인접 리스트로 구현할 수 있다.
1. 인접 행렬
인접 행렬이란, 그래프의 정점을 2차원 배열로 만든것이다.
정점 간에 직접 연결이 되어 있다면 1, 아니라면 0을 저장한다.
장점
- 2차원 배열에 모든 정점의 간선 정보가 담겨있기 때문에 두 정점에 대한 연결을 조회할 때 O(1)의 시간복잡도를 가진다.
- 인접 리스트에 비해 구현이 쉽다.
단점
- 모든 정점에 대해 간선 정보를 입력해야 하므로 인접 행렬을 생성할 때는 O(n제곱)의 시간 복잡도가 소요된다.
- 2차원 배열이 필요하기에 필요 이상의 공간이 낭비된다.
2. 인접 리스트
그래프의 노드를 리스트로 표현한 것으로, 주로 정점의 리스트 배열을 만들어서 관계를 설정한다.

장점
- 정점들의 연결 정보를 탐색할 때 O(n) 시간 복잡도가 소요된다. (n 은 간선의 갯수)
- 필요한 만큼 공간을 사용하기 때문에 인접 행렬에 비해 상대적으로 공간의 낭비가 적다.
단점
- 특정 두 정점이 연결되어 있는지 확인하기 위해서는 인접 행렬에 비해 시간이 오래 걸린다.
- 구현이 인접 행렬에 비해 어렵다.
728x90
Comments




